Ceci n'est pas une ellipsoid
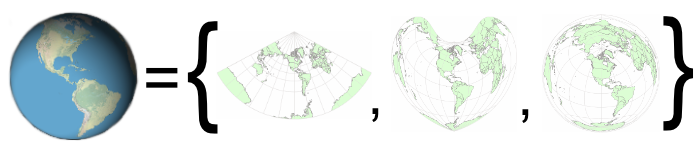
When we work with maps, we must take into account an important thing: we work with maps. This is a more important concept than you can think at first. Think about the Earth; it's spherical (ok, it's not, but at the moment is a good approximation), while the monitor is flat, and paper in which you print maps is flat too. Representing the Earth surface to a map correspond to find a way to map a spherical surface on a plane. If you want, you can try it. Take an orange, and try to make its peel flat.

You can't do it without break it at some point. And, if you tray with more oranges, you can find more ways to try to achieve the result, breaking the peel in different points, for example. At some point you'll see also that you're able to flat a specific portion of the peel, while other parts are more broken/deformed. This is the limit of maps: it's impossible to map a sphere onto a plane without deformations.
It has different consequences. For example, it's not easy to draw by hand a geodesic in a map. The geodesic is the shortest path between two points, and in a spere is not a straight line, because it must lie on the sphere surface. Or calculate the distance between two points by simply using a ruler and the map scale factor.
For this reason there are different type of projections. A projecton is a mathematical law that makes a correspondence between points of earth surface and points of a Cartesian plan. We deform the sphere surface, but in a known way that's an advantage. There are a lot of projection available, and we need to handle them.
In addition to this, the Earth is usually not modelled with a sphere, but with an ellipsoid. In particular, an oblate spheroid, an ellipsoid with two axes with the same length.
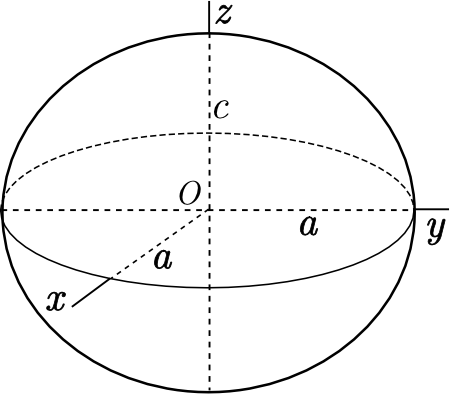
In order to define the ellipsoid, we need to define the major radius and the minor radius, or the major radius and the flatness. In other words, we need two parameters in order to define mathematically the ellipsoid. This leads to a more accurate mathematical representation of the Earth surface, at the cost of more complicated calculus related to surface operations, like calculating the distance between two points (mathematical formulas are in general simpler for spherical surfaces rather than for ellipsoid ones).
In addition to the addition, the Earth is not a mathematical ellipsoid (it can be modelled as geoid, but this is another story). For this reason, different ellipsoid parameters are used, because different nations used different parameter of Earth radii in order to obtain a better match of the ellipsoid with the part of Earth including their own terrain.
With the advent of the GPS system, a global reference system for ellipsoid began to be used, the WGS84 one, that's used nowadays for representing earth data all over the world. For example OpenStreetMap uses WGS84 as Earth representation of its data.
The conclusion of this introduction is that we have different mathematical representation of the Earth surface, using map projections, ellipsoids and so on, and in order to perform operations with Earth data, we need to choose one of these. And here is where we need SRID. It means Spatial Reference Identifier, and it's a numerical value that identifies the type of projection/ellipsoid used for calculus, and its parameters.
ID's and corresponding parameters are defined by a standard created by the Open Geospatial Consortium that maintain it updated.
SRID in PostGIS
When we create an empty database in Postgres and we enable the PostGIS extension, a table named spatial_ref_sys is created. It contains all data needed by PostGIS in order to use SRID properly. For example, we can see what contains this table for the SRID 4326, that's the one used for defining the WGS84 coordinate system:
# SELECT * FROM spatial_ref_sys WHERE srid = 4326; srid | auth_name | auth_srid | srtext | proj4text ------+-----------+-----------+------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------+-------------------------------------- 4326 | EPSG | 4326 | GEOGCS["WGS 84",DATUM["WGS_1984",SPHEROID["WGS 84",6378137,298.257223563,AUTHORITY["EPSG","7030"]],AUTHORITY["EPSG","6326"]],PRIMEM["Greenwich",0,AUTHORITY["EPSG","8901"]],UNIT["degree",0.0174532925199433,AUTHORITY["EPSG","9122"]],AUTHORITY["EPSG","4326"]] | +proj=longlat +datum=WGS84 +no_defs (1 ROW)
We can see that in the table there are different columns:
- srid: This is the primary keiy, and of course it contains the ID that we want to analyse, the 4326 in this case;
- auth_name: This is the name of the author that created the row. In this case the EPSG Geodetic Parameter Dataset;
- auth_srid: This is the SRID referred to the author dataset. Just to know it (I didn't found any use for it at the moment);
- srtext: This is slight more complicated. It's a long string, that represent a string description of the coordinate system, in WKT format;
- proj4text: In PostGIS the different projections are calculated using a library named proj4. The library allows to set different projections and reference systems. It's possible to parse a string with specific parameters in order to set the reference system that can be used. This column contains the string read from the library in order to set the projection defined by the SRID.
We can see the srtext in more detail. Maybe it's a little more clear if we format it:
GEOGCS[
"WGS 84",
DATUM[
"WGS_1984",
SPHEROID[
"WGS 84",
6378137,
298.257223563,
AUTHORITY[
"EPSG",
"7030"
]
],
AUTHORITY[
"EPSG",
"6326"
]
],
PRIMEM[
"Greenwich",
0,
AUTHORITY[
"EPSG",
"8901"
]
],
UNIT[
"degree",
0.0174532925199433,
AUTHORITY[
"EPSG",
"9122"
]
],
AUTHORITY[
"EPSG",
"4326"
]
]
We can see that's the string define a GEOGCS, that's a Geographic Coordinate System. It's a coordinate system that works with latitudes and longitudes. This coordinate system takes four parameters:
- DATUM: This describe the coordinate system. In this case we use a spheroid, that's an ellipsoid that has two axis with the same length. The datum has some parameter in order to be defined:
- The name off the datum;
- The length of semi-major axis, in meters;
- Inverse of the flattening;
- Authority that defined the datum.
- PRIMEM: This is the prime meridian, the one uses as origin for calculus. It's defined by following parameters:
- A string with the name;
- The value of the prime meridian;
- Authority that defined the meridian.
- UNIT: This parameter defines the unit that's used for latitude and longitudes. So it's the unit of measure of an angle. Computers works well with radians, so this parameter defines how to convert the unit of measure used by the coordinate system to radians. We have here:
- The name of the unit of measure. In this case we want to use degrees (even if it's only a name not used in calculus);
- Multiplier that allows to convert the used measure unit to radians (in this case the constant for converting degrees to radians);
- Authority that defined the unit.
- AUTHORITY: Description of the authority that defined the coordinate system. Parameters are:
- Name of the authority;
- SRID used by the authority.
So we have a complete description of the coordinate system that's used in this case.
Example with different SRIDs
Let's see why it's important. We want to calculate the distance between two cities, Palermo (38.115556N, 13.361389E) and Catania (37.502669N, 15.087269E).
Since we want to calculate distances, we'll use directly the data without storing them into the database. The PostGIS function for calculating the distance is ST_Distance.
So open the psql console, and open the database (we don't store data but we need the PostGIS extension, so a PostGIS database is always necessary):
# SELECT ST_Distance(ST_Transform(ST_SetSRID(ST_MakePoint(13.361389, 38.115556), 4326), 2100), ST_Transform(ST_SetSRID(ST_MakePoint(15.087269, 37.502669), 4326), 2100)); st_distance ------------------ 167967.238476883 (1 ROW)
In this query we created a point in an ellipsoid (4326, the WGS84 one) and then we projected this point into a map projection with SRID 2100 (a Greek Grid).
Now we perform the same calculus, but we change the projection:
# SELECT ST_Distance(ST_Transform(ST_SetSRID(ST_MakePoint(13.361389, 38.115556), 4326), 5659), ST_Transform(ST_SetSRID(ST_MakePoint(15.087269, 37.502669), 4326), 5659)); st_distance ------------------ 166881.707299786 (1 ROW)
In this case we projected points in a transverse mercator projection centered in Italy. As you can see, there's a difference in distances.
So, when you work with data, and you need to perform calculus on a projection, it's important to select the right one, that approximates well the area of interest and minimize deformations.
Conclusions
In this article we've seen a little introduction to SRID, and how projection distorsion can affect some calculus, and so the importance of using the right projection depending of the zone of interest of the database. We've also seen a global reference system defined by ellipsoid like WGS84 ones.
Now we're able to work with right data and right projections. We'll see more practical examples in next articles. For now that's all.